Γράφουν οι Φραγκίσκος Αρχοντάκης και Νίκος Χ. Βαρσακέλης*

Για την πρόβλεψη της εξέλιξης μιας πανδημίας χρησιμοποιούνται μαθηματικά και στατιστικά υποδείγματα στα οποία εισάγονται πραγματικά δεδομένα, όπως ο αριθμός των κρουσμάτων, των διασωληνωμένων, των θανάτων, κλπ. Στην πανδημία του Covid-19 ο αριθμός των κρουσμάτων δεν προέρχεται από τυχαία δειγματοληψία και κατά συνέπεια η πρόβλεψη είναι δυσκολότερη. Αντίθετα, ο αριθμός των θανάτων και ο αριθμός των διασωληνωμένων ασθενών μπορούν να χαρακτηρισθούν ως ισχυρά δεδομένα και η πρόβλεψη της εξέλιξής τους μπορεί να είναι καλύτερη. Για τον λόγο αυτό προχωρήσαμε στην εκτίμηση της συσχέτισης του αριθμού των θανάτων με τον αριθμό των διασωληνωμένων.

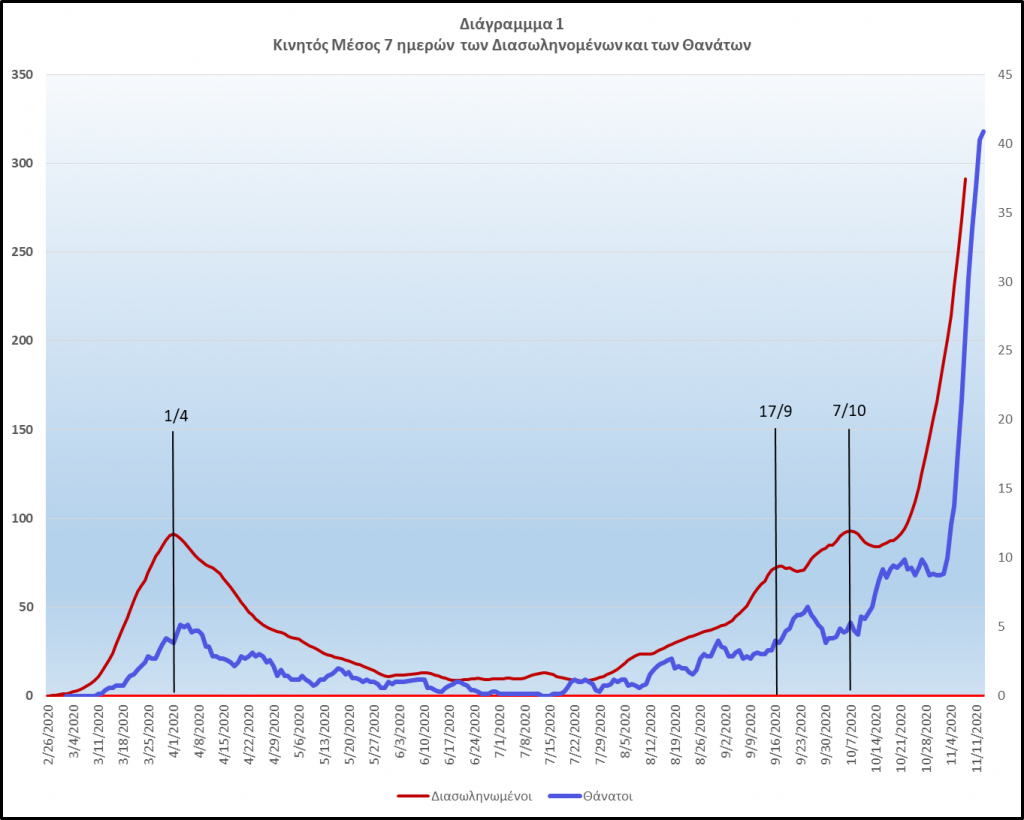
Στο διάγραμμα 1 παρουσιάζεται ο κινητός μέσος όρος των 7 ημερών για τον αριθμό των διασωληνωμένων και των θανάτων. Η συμπεριφορά του κινητού μέσου δείχνει ότι ο αριθμός των διασωληνωμένων προηγείται του αριθμού των θανάτων. Όμως, μια αρκετά ενδιαφέρουσα παρατήρηση είναι ότι ενώ την κορύφωση του αριθμού των διασωληνωμένων της 1ης  Απριλίου ακολουθήσε η κορύφωση των θανάτων μετά από 3 ημέρες, την κορύφωση της 17ης Σεπτεμβρίου ακολούθησε η κορύφωση των θανάτων μετά από 8 ημέρες και την κορύφωση της 7ης Οκτωβρίου ακολούθησε η κορύφωση των θανάτων στις 22 Οκτωβρίου, δηλαδή, μετα από δυο περίπου εβδομάδες. Αυτή η συμπεριφορά ίσως εξηγείται από την θέση που εξέφρασαν πολλοί γιατροί ότι έχει αποκτηθεί σημαντική εμπειρία διαχείρισης της ασθενείας στις ΜΕΘ και έτσι ενώ φαίνεται ότι τον Απρίλιο οι θάνατοι συνέβαιναν πιο γρήγορα, τώρα έχει παραταθεί η ζωή μέσα στις ΜΕΘ, με πιθανό αποτέλεσμα να έχουμε και βελτίωση της υγείας των ασθενών με την καλύτερη αντιμετώπιση.

Για να ελέγξουμε την συσχέτιση μεταξύ του αριθμού των  διασωληνωμένων και των θανάτων χρησιμοποιήσαμε δυο στατιστικές μεθοδολογίες: α) ένα υπόδειγμα χρονολογικών σειρών με χρονικές υστερήσεις του αριθμού των διασωληνωμένων και ανεξάρτητη μεταβλητή τον αριθμό των θανάτων και β) ένα υπόδειγμα αρνητικής διωνυμικής με τις ίδιες μεταβλητές.

Ανάλυση χρονολογικών σειρών

Η ανάλυση χρονολογικών σειρών (time series analysis) μελετά μεταβλητές/συστήματα που εξελίσσονται χρονικά. Στην οικονομική επιστήμη, η ανάλυση χρονολογικών σειρών αναπτύχθηκε για να καλύψει τις ανάγκες για έγκυρες προβλέψεις. Στην συνέχεια η ανάλυση χρονολογικών σειρών επεκτάθηκε και σε άλλα επιστημονικά πεδία, όπως, για παράδειγμα, στην επιδημιολογία. Στο παρόν άρθρο παρουσιάζουμε τα συμπεράσματα μιας προκαταρκτικής ανάλυσης της χρονολογικής σειράς του αριθμού των θανάτων ως συνάρτηση του αριθμού των διασωληνωμένων λόγω Covid-19.

Στην συνάρτηση που εκτιμήθηκε, ως επιδραστικές μεταβλητές ελήφθησαν, μεταξύ άλλων, οι χρονικές υστερήσεις των διασωληνωμένων λόγω Covid-19 μίας εβδομάδας, δυο εβδομάδων, τριών εβδομάδων και τεσσάρων εβδομάδων. Το υπόδειγμα προσεγγίζει σε αρκετά ικανοποιητικό βαθμό τις πραγματικές τιμές, όπως φαίνεται στο διάγραμμα 2.

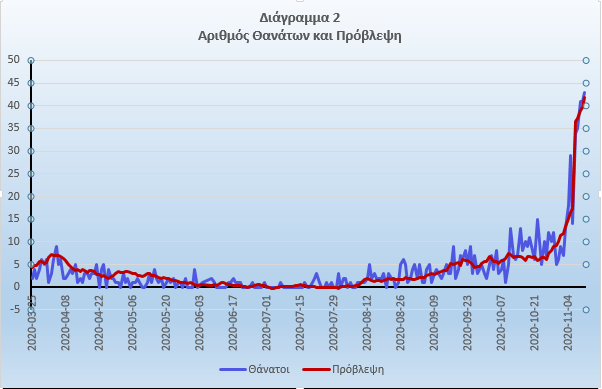
Το εκτιμημένο μοντέλο έδειξε ότι ο αριθμός των θανάτων συσχετίζεται θετικά με τον αριθμό των διασωληνωμένων μιας εβδομάδας και τεσσάρων εβδομάδων. Αντίθετα, ο αριθμός των διασωληνωμένων με χρονική υστέρηση δύο και τριών εβδομάδων δεν είναι στατιστικά σημαντικός. Αυτά τα αποτελέσματα δείχνουν ότι οι ασθενείς που διασωληνώνονται καταλήγουν στο αρχικό στάδιο της νοσηλείας ή στις 4 εβδομάδες. Αντιθέτως, φαίνεται πως στις 2-3 εβδομάδες παρατηρείται: α) αφενός μεν η συνέχιση της «μάχης για τη ζωή» που δίνουν οι ασθενείς και το προσωπικό των ΜΕΘ να κρατηθούν οι ασθενείς στην ζωή και β) αφετέρου ένας αριθμός διασωληνωμένων τα καταφέρνει και κερδίζει την μάχη της ζωής, όπως είπε και η κ. Κοτανίδου. Όμως η στατιστική σημαντικότητα της τέταρτης εβδομάδας δείχνει ότι εάν ένας ασθενής παραμείνει για μεγάλο διάστημα στην ΜΕΘ, η πιθανότητα να τα καταφέρει μειώνεται σημαντικά.

Υπόδειγμα Παλινδρόμησης με Αρνητική Διωνυμική

Για να ελέγξουμε τα αποτελέσματα της ανάλυσης των χρονολογικών σειρών προχωρήσαμε και στην εφαρμογή μιας δεύτερης μεθόδου. Η αρνητική διωνυμική κατανομή (Negative Binomial) είναι μια διακριτή συνάρτηση κατανομής που μπορεί να χρησιμοποιηθεί για να δώσει καλύτερα αποτελέσματα από την κατανομή Poisson, επιτρέποντας μέση τιμή και διακύμανση να είναι διαφορετικές, σε αντίθεση με την Poisson. Στην επιδημιολογία, η αρνητική διωνυμική κατανομή έχει χρησιμοποιηθεί για την μοντελοποίηση της μετάδοσης ασθενειών από μολυσματικές ασθένειες, όπου ο πιθανός αριθμός μεταγενέστερων λοιμώξεων μπορεί να ποικίλλει σημαντικά από άτομο σε άτομο (για παράδειγμα, ο αναγνώστης μπορεί να ανατρέξει σε αυτό το άρθρο στο Nature ).

Τα αποτελέσματα που πήραμε από την εφαρμογή της αρνητικής διωνυμικής για την συσχέτιση του αριθμού των θανάτων με τον αριθμό των διασωληνωμένων είναι παρόμοια με αυτά της ανάλυσης των χρονολογικών σειρών. Στατιστικά σημαντικοί (και με θετικό πρόσημο) είναι οι συντελεστές για την 1η εβδομάδα και για την 4η εβδομάδα ενώ κατά τη 2η εβδομάδα φαίνεται πως ο αριθμός θανάτων πέφτει (ο συντελεστής είναι στατιστικά σημαντικός με αρνητικό πρόσημο).

Συνεπώς, καθώς τα κρούσματα θα μειώνονται λόγω του απαγορευτικού, λόγω του υψηλού αριθμού των διασωληνωμένων αυτές τις μέρες θα πρέπει να αναμένουμε αυξημένο αριθμό θανάτων μέχρι και τέσσερις εβδομάδες μετά την κορύφωση του αριθμού των διασωληνωμένων, με μια ενδεχόμενη ύφεση ενδιάμεσα, ceteris paribus.

Τέλος, οι μεθοδολογίες και τα αποτελέσματα που πήραμε αντανακλούν τα στατιστικά δεδομένα και σε καμία περίπτωση δεν πρέπει να εκληφθούν ως ιατρικό αποτέλεσμα ότι, δηλαδή, εάν ένας ασθενής ξεπεράσει τις 7 μέρες ξεπέρασε το πρόβλημα ή εάν φτάσει στην τέταρτη εβδομάδα παραμονής στην ΜΕΘ πρέπει να θεωρείται ότι έχασε την μάχη για την ζωή.

*O Φραγκίσκος Αρχοντάκης είναι λέκτορας της Σχολής Ανθρωπιστικών, Κοινωνικών και Οικονομικών Επιστημών στο Διεθνές Πανεπιστήμιο, ενώ ο Νίκος Χ. Βαρσακέλης είναι καθηγητής Βιομηχανικής Πολιτικής στο Τμήμα Οικονομικών Επιστημών του Αριστοτελείου Πανεπιστημίου Θεσσαλονίκης.