«Λατρεύω τη φυσική» συνήθιζε να λέει. Και εκδηλωνόταν με πολλή ζέση για ένα θέμα το οποίο συνήθως δεν ενθουσιάζει τους μη ειδικούς. Εγραψε μάλιστα ότι ήθελε να βρει έναν τρόπο να μεταφέρει στα έργα του την αντι-ύλη. «Είναι θέμα μιας νέας εξίσωσης που διατύπωσε ο δρ Βέρνερ Χάιζενμπεργκ, η οποία μπορεί να δώσει τον τύπο της ενότητας της ύλης» – και τα έγραφε αυτά στο «Μανιφέστο περί αντι-ύλης». Ποιος; Ο ισπανός ζωγράφος Σαλβαντόρ Νταλί, που έζησε από το 1904 ως το 1989 και εκτός από τους πίνακές του μας άφησε τα παραπάνω στο «Μανιφέστο περί αντι-ύλης», ενώ ζωγράφισε και έναν πίνακα με τίτλο «Αντιπρωτονική ανάληψη», γράφοντας στο «Ημερολόγιο μιας μεγαλοφυΐας»: «H Παρθένος δεν ανέρχεται στους ουρανούς από τη δύναμη της προσευχής αλλά από αυτή καθαυτή τη δύναμη των αντιπρωτονίων της».
Στα βιβλιοπωλεία εμφανίστηκε ήδη μια διπλωματική εργασία που εκπονήθηκε από τη Μαρία Θωμά σχετικά με κάποιους πίνακες του Νταλί και με τον απροσδόκητο υπότιτλο «H κβαντομηχανική και η Θεωρία της Σχετικότητος μέσα από το έργο του μεγάλου σουρεαλιστή». H ενδιαφέρουσα αυτή εργασία, που βγήκε από τις εκδόσεις Ελάτη, μαζί με μια έκθεση έργων του ουγγρικής καταγωγής διάσημου γάλλου καλλιτέχνη Βικτόρ Βασαρελί στο Herakleidon, Experience in Visual Arts, στο Θησείο, μας δίνει την ευκαιρία να παρουσιάσουμε και τα αποτελέσματα μιας ευρύτερης δικής μας έρευνας για το πώς μεγάλοι ζωγράφοι έχουν επηρεαστεί από διάφορες επιστημονικές θεωρίες. Αλλά και αντίστροφα, χρησιμοποιώντας κάποιους πίνακες γίνεται φανερό ότι θα μπορούσαμε να κινήσουμε το ενδιαφέρον ανθρώπων που θέλουν να ζωγραφίσουν, για περιοχές της γνώσης εκ πρώτης όψεως αρκετά δυσπρόσιτες.
Οπως παρατηρεί το περιοδικό «Nature» (22.9.2005, σελ. 482), όταν η Βασιλική Ακαδημία των Καλών Τεχνών, που μόλις είχε ιδρυθεί, διόριζε τον Γουίλιαμ Χάντερ, τον μαιευτήρα της βασίλισσας, ως τον πρώτο καθηγητή της Ανατομίας, το 1769, συνέχιζε μια παράδοση που είχε αρχίσει στην Κεντρική Ευρώπη από τον 16ο αιώνα. Οι σχολές καλών τεχνών δίδασκαν με τη βοήθεια ειδικών καθηγητών θεωρία της προοπτικής, ανατομία και άλλα επιστημονικά θέματα, θέλοντας να μη μένουν οι μέλλοντες ζωγράφοι απλοί τεχνίτες με μοναδικό εργαλείο τους το χρώμα. Υπάρχει μάλιστα και πίνακας της εποχής όπου εμφανίζεται ο Χάντερ να κάνει μάθημα στους φοιτητές της σχολής χρησιμοποιώντας κούκλα, σκελετό, αλλά και έναν… κατάδικο, που ήταν το ζωντανό του πρότυπο για τις ανάγκες των μαθημάτων. Παρών φαίνεται να είναι και ο διευθυντής της σχολής, σε ρόλο παρατηρητού (ο κύριος στο κέντρο με το ακουστικό στο αφτί), διότι είχε τότε προκύψει μείζον θέμα με τις αντικαλλιτεχνικές θεωρίες του ανατόμου περί ανωτερότητος των έργων της φύσης σε σχέση με τις δημιουργίες των καλλιτεχνών. Ασχετα όμως από αυτό, έχουμε μια ένδειξη ότι από τότε κάποιοι το έβρισκαν άκρως ωφέλιμο να ενημερώνονται οι νέοι καλλιτέχνες και για θέματα άλλων επιστημών.
Μπορούμε να δούμε στο εσωτερικό των απειροελάχιστα μικρών ατόμων με τα μάτια ενός ανθρώπου; Ή να κατανοήσουμε πώς θα ήταν ένα από τα συνηθισμένα γεωμετρικά σώματα του κόσμου μας σε έναν άλλο, τετραδιάστατο κόσμο; Μήπως αντικείμενα της μαθηματικής σκέψης όπως η φιάλη του Klein μάς προτρέπουν να ανοιχθούμε προς άλλες προσεγγίσεις αυτού που θεωρούμε δεδομένη πραγματικότητα; Αν δεχθούμε ότι η φυσική είναι μια γλώσσα που επινόησαν οι άνθρωποι θέλοντας να μιλήσουν για τον κόσμο και μια πρόταση για το πώς θα μπορούσε να νοηθεί η δομή του κόσμου, η ζωγραφική θα μπορούσε να βοηθήσει ακριβώς εκεί όπου σταματάει η ικανότητά μας να βάλουμε τη δομή αυτή σε λέξεις. Κυρίως τώρα που έχουμε προχωρήσει τόσο στον μικρόκοσμο των ηλεκτρονίων, των πρωτονίων, των νετρονίων και του εσωτερικού τους, μετά την ανακάλυψη και των κουάρκ. Μόνο με όρους μαθηματικούς μπορούμε να αντιμετωπίσουμε τα κουάρκ; Υπάρχουν καλλιτέχνες, αλλά και άνθρωποι των λεγομένων θετικών επιστημών, που πιστεύουν ότι και η τέχνη μπορεί να συνεργαστεί με τη φυσική και τα μαθηματικά. Αλλωστε δεν είναι και τόσο… ξένοι μεταξύ τους.
Από τον καιρό του Πλάτωνα (427-348 π.X.), κυρίως από το έργο του «Τίμαιος», ήταν γνωστό ότι μόνο πέντε κυρτά πολύεδρα μπορούσαν να υπάρχουν στον χώρο των τριών διαστάσεων. Αυτά ονομάστηκαν Πλατωνικά Στερεά και οι ιδιότητές τους θεμελιώθηκαν από τον Ευκλείδη το 300 π.X., ενώ ο Αρχιμήδης ανακάλυπτε και άλλα πολύεδρα, φθάνοντας τον αριθμό τους στα δεκατρία. Στα μέσα του 15ου αι. ο ιταλός ζωγράφος Πάολο Ουτσέλο δουλεύοντας για τη Βασιλική του Αγίου Μάρκου βρήκε και άλλα πολύεδρα, που όλα διατηρούν τις ρίζες των πέντε αρχικών πλατωνικών στερεών. Στη διάρκεια του 15ου αι., ενώ η βυζαντινή ζωγραφική επέμενε να μένει θρησκευτική και μονοδιάστατη, δίνοντας βάρος περισσότερο στο (θεολογικό της) περιεχόμενο παρά στη μορφή, η κατεύθυνση της ζωγραφικής στη Δύση, αντίθετα, ήταν κυρίως στο πώς ο χώρος των τριών διαστάσεων θα απεικονιστεί στο επίπεδο του πίνακα. Ετσι έχουμε εκεί προς το τέλος, το 1482, το κλασικό έργο του Πιέρο ντέλα Φραντσέσκα, ενός ζωγράφου που θεωρείται όχι μόνο ένας από τους καλύτερους μαθηματικούς, αλλά και εμπειρογνώμων στις γεωμετρικές και μαθηματικές τεχνικές για τη δημιουργία της αίσθησης της προοπτικής και κατ’ επέκταση της τρισδιάστατης εικόνας. Ας μην ξεχνάμε ότι τότε ήταν αυτονόητο οι ζωγράφοι να γνωρίζουν και αρκετά από τα μαθηματικά της εποχής τους. Ως τον 19ο αι. οι αναζητήσεις περιορίστηκαν στα περί προοπτικής, αλλά ακολουθώντας την άνθηση των μαθηματικών οι εξελίξεις έγιναν πιο συναρπαστικές. Εμφανίστηκαν οι μη ευκλείδειες γεωμετρίες που καταπιάστηκαν με τον πραγματικό χώρο γύρω μας και όχι τον εξιδανικευμένα επίπεδο ευκλείδειο χώρο, καταργώντας κάποια από τα αξιώματα του Ευκλείδη και επιμένοντας π.χ. στο ότι ένα τρίγωνο, απλωμένο επάνω στη γήινη σφαίρα, θα έχει και άθροισμα γωνιών πάνω από 180 μοίρες.
Στο τέλος του 19ου αι. και στις αρχές του 20ού αι. εμφανίζονται οι θεωρίες του Αϊνστάιν που προσέθεταν μια τέταρτη διάσταση στις τρεις ως τότε παραδεκτές, αυτήν του χωροχρόνου, και οι προχωρημένοι καλλιτέχνες διχάζονται στην προσπάθειά τους να αφομοιώσουν τις νέες επιστημονικές θεωρίες. Ο Πικάσο και ο Νταλί δημιουργούν πάνω στις θεωρίες του Αϊνστάιν και του γερμανού μαθηματικού Ρίμαν. Ο Πικάσο παρουσιάζει στις «Δεσποινίδες της Αβινιόν» τη μία από αυτές σαν ένα σώμα στις τέσσερις διαστάσεις, ενώ ο Νταλί στο «Corpus Hypercubus» έχει τον Ιησού Χριστό σταυρωμένο επάνω σε έναν υπερκύβο, σώμα που θα συναντούσαμε μόνο αν ζούσαμε σε έναν κόσμο με τέσσερις διαστάσεις. Για άλλους καλλιτέχνες, όπως οι ντανταϊστές, οι σοβιετικοί κονστρουκτιβιστές με επικεφαλής τον Μαλέβιτς είδαν στις μη ευκλείδειες γεωμετρίες τη δυνατότητα απελευθέρωσης από τις δεσμεύσεις του χώρου μας καταργώντας τα περί προοπτικής. Ντυσάμπ, Μοντριάν, Καντίνσκι ήταν μερικοί από τους πιο γνωστούς καλλιτέχνες που προσπάθησαν να συνδυάσουν επιστήμη και ζωγραφική, ενώ είναι χαρακτηριστικός ο τίτλος ενός έργου του Υβ Τανγκί: «H συνάντηση των παραλλήλων». Προχωρώντας στον 20ό αι. οι εικαστικοί καλλιτέχνες προσπαθούν να εξερευνήσουν και τον αισθητό κόσμο και τον νοητικό αλλά και έναν τρίτο, αυτόν των τυχαίων μα στέρεα δομημένων γεγονότων, που υλοποιούνται από τις «πολύχρωμες σταγόνες» τις ριγμένες σαν βροχή σε οριζόντιο καμβά με εκπληκτική μαεστρία από τον Τζάκσον Πόλοκ, ενώ στη συνέχεια απέκτησαν και νόμους χάρη στον Μάντελμπροτ και στις περί Χάους θεωρίες. Και μέσα από τις ίδιες θεωρίες, αλλά με αντίθετη εντελώς προσέγγιση ως προς τον τρόπο δημιουργίας, προέκυψε το έργο του Εσερ, γεμάτο από σχέδια που όσο κι αν τα δεις σε μικρότερη κλίμακα μένουν τα ίδια, άρα έχουν μια φράκταλ δομή, αδύνατες κατασκευές, αλλά και μια χειροπιαστή υλοποίηση εννοιών όπως η ταινία του Μέμπιους, που ανήκει σε έναν ξεχωριστό κλάδο των μαθηματικών, την τοπολογία. Εναν κλάδο που ασχολείται με το ποιες ιδιότητες διατηρούνται όταν ένα σώμα ή μια επιφάνεια υφίστανται κάποιες παραμορφώσεις αλλά όχι σχίσιμο, τρύπημα, σπάσιμο. Λένε ότι ένας τοπολόγος θεωρεί «ομοιομορφικά» ένα φλιτζάνι με χερούλι και έναν λουκουμά ντόνατ, αφού και τα δύο έχουν μία οπή στη μέση, ή έναν κύκλο και ένα τετράγωνο, αφού μπορούμε να φθάσουμε από το ένα στο άλλο παραμορφώνοντας κάποια τμήματά τους. H τοπολογία ενδιαφέρεται για σχήματα όπως η ταινία του Μέμπιους, που είναι μια λωρίδα της οποίας ενώσαμε τα άκρα αφού τη στρίψαμε μία φορά. Και έχει την εξής ιδιότητα: αν ξεκινήσουμε να τη βάφουμε με ένα πινέλο, προχωρώντας θα έχουμε στο τέλος βάψει και τις δύο επιφάνειές της χωρίς να χρειαστεί να διακόψουμε το βάψιμο για να αλλάξουμε επιφάνεια. Είναι, όπως λέει η τοπολογία, επιφάνεια μιας μόνον πλευράς. Και το ίδιο συμβαίνει, όσο κι αν φαίνεται παράξενο, με τη φιάλη Klein, ένα μπουκάλι του οποίου το στόμιο το λυγίζουμε και το βυθίζουμε ξανά στο εσωτερικό του. Τέτοια σχήματα έχουν εμπνεύσει πολλούς καλλιτέχνες, από τον Ολλανδό Εσερ ως τον Αμερικανό Κόλινς, αποδεικνύοντας πόσο γόνιμα τα μαθηματικά μπορούν να επηρεάσουν την καλλιτεχνική δημιουργία.
Μαθήματα φυσικής στη Σχολή Καλών Τεχνών; Μαθήματα ζωγραφικής στη Φυσικομαθηματική Σχολή; Γιατί όχι; O Βασαρελί έγραψε: «Καταβρόχθισα αμέτρητα βιβλία για τη Σχετικότητα, την κβαντομηχανική, την κυβερνητική, την αστροφυσική. Μια φράση μού έκανε βαθιά και μόνιμη εντύπωση: “την ύλη μπορούμε να τη δούμε και σαν ενέργεια και κατ’ επέκταση σαν παραμόρφωση του χώρου”. H θεωρητική φυσική ξαφνικά αποκαλύφθηκε σ’ εμένα σαν μια νέα πηγή ποιητικής έμπνευσης».
Ο πίνακας του Σαλβαντόρ Νταλί «Christus Hypercubus» από το 1954, που βρίσκεται στο Μητροπολιτικό Μουσείο Τέχνης της Νέας Υόρκης, είναι ένα κλασικό παράδειγμα όπου ο καλλιτέχνης δημιουργώντας το έργο του είχε επηρεαστεί και από μαθηματικές θεωρίες της εποχής. Και αυτό είναι σημαντικό για την καλύτερη κατανόηση των όσων απεικονίζει ο πίνακας. Στη συγκεκριμένη περίπτωση ο Χριστός είναι καθηλωμένος σε μια κατασκευή η οποία μοιάζει με σταυρό αλλά για όσους ξέρουν είναι το πώς φαντάζονται οι μαθηματικοί ότι θα φαινόταν από εμάς που ζούμε στις τρεις διαστάσεις ένας «υπερκύβος», δηλαδή ένας κύβος δομημένος στον χώρο των τεσσάρων διαστάσεων. Εννοείται ότι η υπερβατικότητα του έργου γίνεται κατανοητή όταν γνωρίζουμε κάποια πράγματα περισσότερα περί υπερκύβων και χώρων με διαστάσεις μεγαλύτερες των τριών. Ο υπερκύβος στον οποίο είναι καθηλωμένος ο Χριστός όταν προβάλλεται στις τρεις διαστάσεις παίρνει το σχήμα του σταυρού
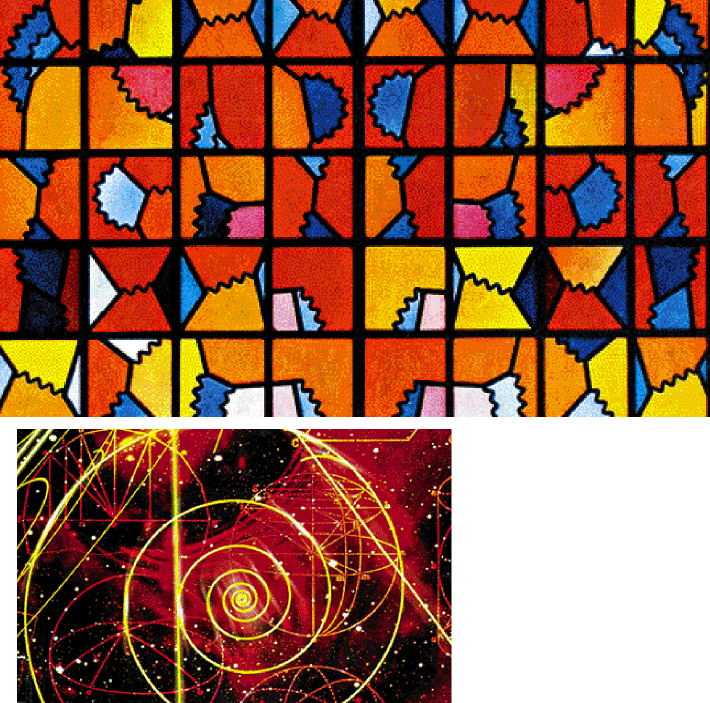
Αντιπροσωπευτικοί πίνακες αυτής της έκθεσης θα ήταν και οι: * «Εναστρη νύχτα πάνω από την πόλη Ρον», Βικέντιος βαν Γκογκ * «Ελεύθερη πτώση», Χούλιο Γκονζάλες, 1993 * «Ταινία Μέμπιους II», Μάουριτς Κορνέλις Εσερ * «Τετραγωνικό όριο», Μάουριτς Κορνέλις Εσερ * «Αμερικανικός γοτθισμός», Γκραντ Γουντ, 1930 * Ατιτλοφόρητο μωσαϊκό, Πάολο Ουτσέλο, 1425-1430 * Γραμμική κατασκευή στον χώρο Νο. 1, Ναούμ Γκάμπο * Βιτρό με διαγράμματα Feynman(!) στην εκκλησία του Αγίου Νικολάου στη γερμανική κωμόπολη Καλκάρ, Καρλ Μάρτιν Χάρτμαν * «Corpus Hypercubus», Σαλβαντόρ Νταλί, 1935 * «Μια καλοκαιρινή Κυριακή», Ζορζ Σερά, 1884-46 * Ο Νταλί γυμνός, «Σωματιδιακό κύμα», Ντόουν Μέσον * «Κβάζαρ», Βικτόρ Βασαρελί * Σχέδιο για ταπέτο με υπολογιστή, Πασόχα και Λακχτάκια
«Λευκό σπίτι τη νύχτα», Βικέντιος βαν Γκογκ
«Φιάλη του Κλάιν», κατασκευή σε γυαλί του Αλαν Μπένετ
Εργο Νο. 14, Τζάκσον Πόλοκ
«H μαστίγωση του Χριστού», Πιέρο ντέλα Φραντσέσκα
«Print Gallery», Μάουριτς Κορνέλις Εσερ
«Οι δεσποινίδες της Αβινιόν», Πάμπλο Πικάσο